Enginius/Machine Learning
Gaussian Process를 이용한 mu, dmu, ddmu 구하기
해리s
2021. 2. 1. 02:24
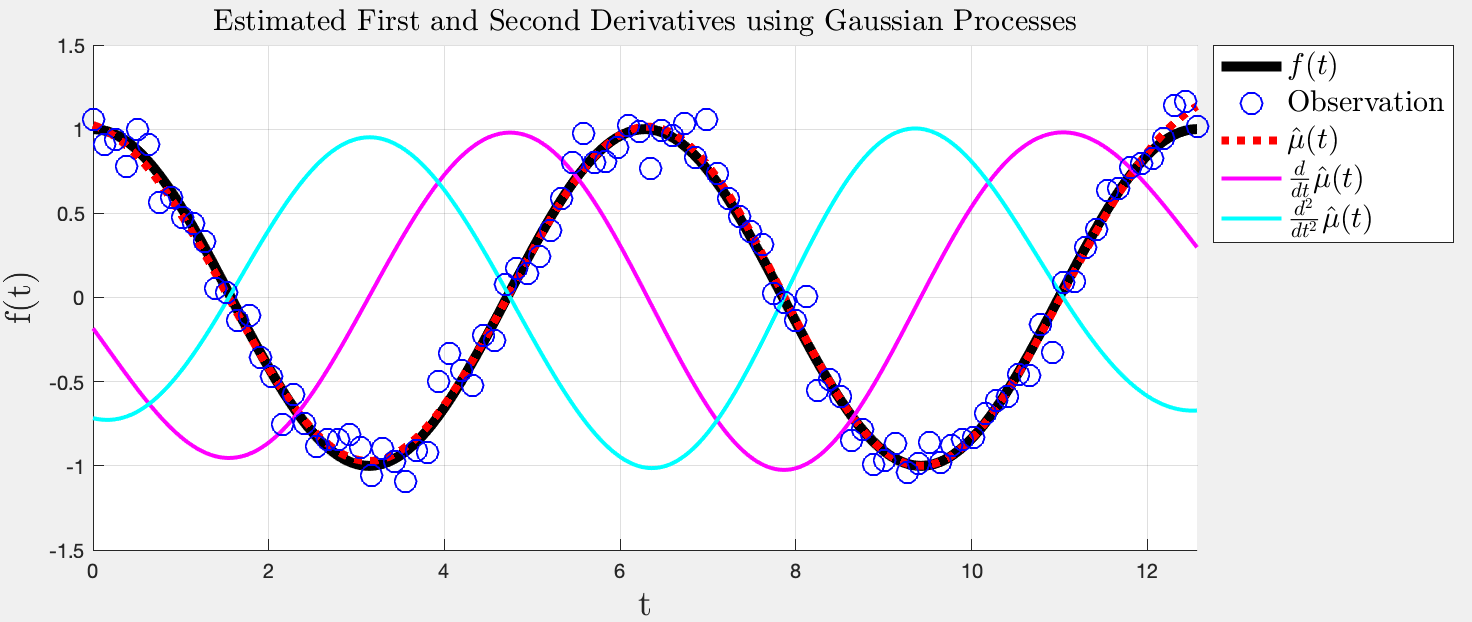
위와 같은걸 할 수 있다.
GP의 mean은 kernel에 따라 미분 가능하다.
% Reference data
f_ref = @(x)( cos(x) ); % reference function
t_max = 4*pi;
t_ref = linspace(0,t_max,1000)';
x_ref = f_ref(t_ref);
% Anchor dataset (training data)
n_anchor = 100;
t_anchor = linspace(0,t_max,n_anchor)';
noise_var = 1e-2;
x_anchor = f_ref(t_anchor) + sqrt(noise_var)*randn(size(t_anchor));
l_anchor = ones(n_anchor,1);
% Gaussian random path
n_test = 1000;
t_test = linspace(0,t_max,n_test)';
hyp = [1,3]; % [gain,len]
[k_test,dk_test,ddk_test] = kernel_levse(t_test,t_anchor,ones(n_test,1),l_anchor,hyp);
K_anchor = kernel_levse(t_anchor,t_anchor,l_anchor,l_anchor,hyp);
% Compute mu, d_mu, and dd_mu
meas_std = 1e-2; % expected noise
mu_test = k_test / (K_anchor+meas_std*eye(n_anchor,n_anchor)) * x_anchor;
dmu_test = dk_test / (K_anchor+meas_std*eye(n_anchor,n_anchor)) * x_anchor;
ddmu_test = ddk_test / (K_anchor+meas_std*eye(n_anchor,n_anchor)) * x_anchor;
% Plot
set_fig(figure(1),'pos',[0.5,0.4,0.5,0.3],...
'view_info','','axis_info',[0,4*pi,-1.5,1.5],'AXIS_EQUAL',0,'GRID_ON',1,...
'REMOVE_MENUBAR',1,'USE_DRAGZOOM',0,'SET_CAMLIGHT',1,'SET_MATERIAL','METAL',...
'SET_AXISLABEL',1,'ax_str','t','ay_str','f(t)','afs',18,'interpreter','latex');
h_ref = plot(t_ref,x_ref,'k-','linewidth',5);
h_mu = plot(t_test,mu_test,'r:','linewidth',4);
h_dmu = plot(t_test,dmu_test,'-','linewidth',2,'Color','m');
h_ddmu = plot(t_test,ddmu_test,'-','linewidth',2,'Color','c');
h_anchor = plot(t_anchor,x_anchor,'bo','linewidth',1,'markersize',11);
legend([h_ref,h_anchor,h_mu,h_dmu,h_ddmu],...
{'$f(t)$','Observation','$\hat{\mu}(t)$',...
'$\frac{d}{dt} \hat{\mu}(t)$','$\frac{d^2}{dt^2} \hat{\mu}(t)$'},...
'fontsize',15,'interpreter','latex','location','NorthEastOutside');
plot_title('Estimated First and Second Derivatives using Gaussian Processes',...
'interpreter','latex','tfs',15);
function [K,dK,ddK] = kernel_levse(X1, X2, L1, L2, hyp)
%
% Leveraged squared exponential kernel
%
d1 = size(X1, 2);
d2 = size(X2, 2);
if d1 ~= d2, fprintf(2, 'Data dimension missmatch! \n'); end
% Kernel hyperparameters
beta = hyp(1); % gain
gamma = hyp(2:end); % length parameters (the bigger, the smoother)
% Make each leverave vector a column vector
L1 = reshape(L1,[],1);
L2 = reshape(L2,[],1);
% Compute the leveraged kernel matrix
x_dists = pdist2(X1./gamma, X2./gamma, 'euclidean').^2;
l_dists = pdist2(L1, L2, 'cityblock');
K = beta * exp(-x_dists) .* cos(pi/2*l_dists);
% First derivative (assume xdim=1)
if nargin >= 1
diff_X = bsxfun(@minus,X1./gamma,(X2./gamma)');
dK = K .* (-2/gamma*diff_X);
end
% Second derivative (assume xdim=1)
if nargin >= 2
ddK = dK .* (-2/gamma*diff_X) + K * (-2/(gamma^2));
end