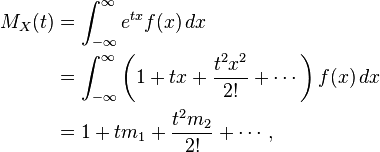출처: http://en.wikipedia.org/wiki/Moment-generating_function , http://en.wikipedia.org/wiki/Normal_distribution
When X~N(u,sigma^2)
then Expectation of X^n can be solved easily using MGF(Moment Generating Function)

| Order | Raw moment | Central moment | Cumulant |
|---|---|---|---|
| 1 | μ | 0 | μ |
| 2 | μ2 + σ2 | σ 2 | σ 2 |
| 3 | μ3 + 3μσ2 | 0 | 0 |
| 4 | μ4 + 6μ2σ2 + 3σ4 | 3σ 4 | 0 |
| 5 | μ5 + 10μ3σ2 + 15μσ4 | 0 | 0 |
| 6 | μ6 + 15μ4σ2 + 45μ2σ4 + 15σ6 | 15σ 6 | 0 |
| 7 | μ7 + 21μ5σ2 + 105μ3σ4 + 105μσ6 | 0 | 0 |
| 8 | μ8 + 28μ6σ2 + 210μ4σ4 + 420μ2σ6 + 105σ8 | 105σ 8 | 0 |
일반적인 경우의 MGF는 다음과 같다.
If X has a continuous probability density function ƒ(x), then MX(−t) is the two-sided Laplace transform of ƒ(x).
여러 분포 함수들의 MGF 는 다음과 같다.
| Distribution | Moment-generating function MX(t) | Characteristic function φ(t) |
|---|---|---|
Bernoulli 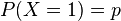 |
 |
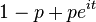 |
Geometric 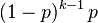 |
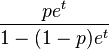 , ,for 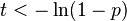 |
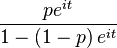 |
| Binomial B(n, p) | 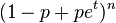 |
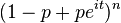 |
| Poisson Pois(λ) | 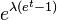 |
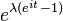 |
| Uniform U(a, b) | 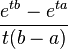 |
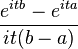 |
| Normal N(μ, σ2) | 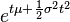 |
 |
| Chi-square χ2k |  |
 |
| Gamma Γ(k, θ) | 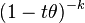 |
 |
| Exponential Exp(λ) |  |
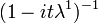 |
| Multivariate normal N(μ, Σ) |  |
 |
| Degenerate δa |  |
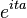 |
| Laplace L(μ, b) |  |
 |
| Cauchy Cauchy(μ, θ) | not defined |  |
| Negative Binomial NB(r, p) | 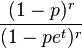 |
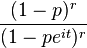 |
'Enginius > Machine Learning' 카테고리의 다른 글
| 퍼셉트론 패턴인식 데모 (0) | 2011.10.25 |
|---|---|
| Introduction to Pattern Recognition (0) | 2011.10.25 |
| using FLDA to classify IRIS data set (0) | 2011.10.14 |
| HMM viterbi algorithm (0) | 2011.10.13 |
| 라그랑즈 미정 계수법을 이용한 최적화 기법 (0) | 2011.10.12 |