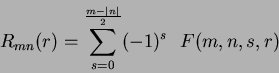본문 바로가기
Enginius/Machine Learning

Complex Zernike moments

해리s 2012. 5. 21. 01:56


The Zernike polynomials were first proposed in 1934 by Zernike [22]. Their moment formulation appears to be one of the most popular, outperforming the alternatives [19] (in terms of noise resilience, information redundancy and reconstruction capability). The pseudo-Zernike formulation proposed by Bhatia and Wolf [3] further improved these characteristics. However, here we study the original formulation of these orthogonal invariant moments.

Complex Zernike moments [18] are constructed using a set of complex polynomials which form a complete orthogonal basis set defined on the unit disc $(x^{2} + y^{2}) \leq 1$. They are expressed as$A_{pq}$Two dimensional Zernike moment: 

\begin{displaymath} A_{mn} = \frac{m+1}{\pi} \int_{x} \int_{y} f(x,y)[V_{mn}(x,y)]^{*} ~dx~dy~~~~~\mbox{where $x^{2} + y^{2} \leq ~1$} \end{displaymath}(49)

where $m = 0,1,2,...,\infty$ and defines the order, $f(x,y)$ is the function being described and $*$ denotes the complex conjugate. While $n$ is an integer (that can be positive or negative) depicting the angular dependence, or rotation, subject to the conditions: 
\begin{displaymath} m- \mid n \mid ~=~even~~,~~\mid n \mid~\leq~m \end{displaymath}(50)

and $A_{mn}^*=A_{m,-n}$ is true. The Zernike polynomials [22] $V_{mn}(x,y)$$V_{mn}(x,y)$Zernike polynomial expressed in polar coordinates are: 
\begin{displaymath} V_{mn}(r,\theta)~=~R_{mn}(r)\exp(jn\theta) \end{displaymath}(51)

where $(r,\theta)$ are defined over the unit disc, $j=\sqrt{-1}$ and $R_{mn}(r)$ is the orthogonal radial polynomial, defined as$R_{mn}(r)$Orthogonal radial polynomial: 
\begin{displaymath} R_{mn}(r) = \sum_{s=0}^{\frac{m-\mid n \mid}{2}}(-1)^{s}~~F(m,n,s,r) \end{displaymath}(52)

where: 
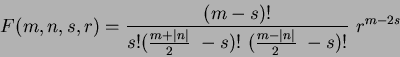\begin{displaymath} F(m,n,s,r) = \frac{(m-s)!}{s!(\frac{m+\mid n \mid}{2}~-s)!~(\frac{m-\mid n \mid}{2}~-s)! }~r^{m-2s} \end{displaymath}(53)

where $R_{mn}(r)=R_{m,-n}(r)$ and it must be noted that if the conditions in Equation 1.50 are not met, then $R_{mn}(r) =~0$. The first six orthogonal radial polynomials are: 
$\displaystyle R_{00}(r) =$$\textstyle 1~~$$\displaystyle ~~R_{11}(r) = r$ 
$\displaystyle R_{20}(r) =$$\textstyle 2r^{2} - 1~~$$\displaystyle ~~ R_{22}(r) = r^{2}$(54)
$\displaystyle R_{31}(r) =$$\textstyle 3r^{3} - 2r~~$$\displaystyle ~~R_{33}(r) = r^{3}$ 

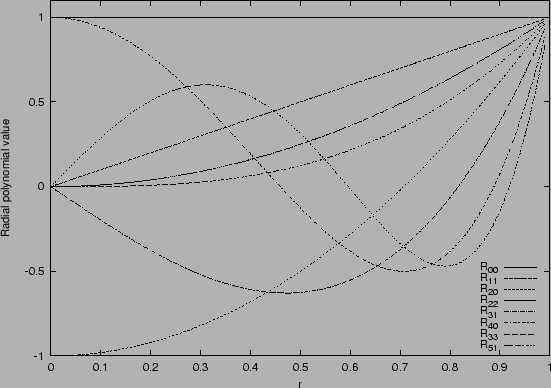
Figure 1.6 shows eight such radial responses, where it can been seen that the polynomials become more grouped, as they approach the edge of the unit disc ($r$ approaches unity). (Care must be taken with regard to the accuracy of these polynomial calculations as the factorial operations can quickly produce large integer values, even at relatively low order $m$). The difference between these orthogonal polynomials and the non-orthogonal monomials can be seen by comparing Figure 1.6 with Figure 1.2.

Figure 1.6: Eight orthogonal radial polynomials plotted for increasing $r$.
\rotatebox{0}{\scalebox{1.0}{\includegraphics{images/theory/radial_polynomial_plots.ps}}}

So for a discrete image, if $P_{xy}$ is the current pixel then Equation 1.49 becomes: 
\begin{displaymath} A_{mn} = \frac{m+1}{\pi} \sum_{x} \sum_{y} P_{xy}[V_{mn}(x,y)]^{*} ~~~~~\mbox{where $x^{2} + y^{2} \leq ~1$} \end{displaymath}(55)

To calculate the Zernike moments, the image (or region of interest) is first mapped to the unit disc using polar coordinates, where the centre of the image is the origin of the unit disc. Those pixels falling outside the unit disc are not used in the calculation. The coordinates are then described by the length of the vector from the origin to the coordinate point, $r$, and the angle from the $x$ axis to the vector $r$$r$Polar co-ordinate radius, $\theta$$\theta$Polar co-ordinate angle, by convention measured from the positive $x$ axis in a counter clockwise direction. The mapping from Cartesian to polar coordinates is: 
\begin{displaymath} x = r~\cos\theta~~~~~~~~y = r~\sin\theta \end{displaymath}(56)

where 
\begin{displaymath} r = \sqrt{x^2 + y^2} ~~~~~~~~ \theta = \tan^{-1}\left(\frac{y}{x}\right) \end{displaymath}(57)

However, $\tan^{-1}$ in practice is often defined over the interval $- \frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}$, so care must be taken as to which quadrant the Cartesian coordinates appear in. Translation and scale invariance can be achieved by normalising the image using the Cartesian moments prior to calculation of the Zernike moments [7]. Translation invariance is achieved by moving the origin to the image's COM, causing $m_{01}=m_{10}=0$. Following this, scale invariance is produced by altering each object so that its area (or pixel count for a binary image) is $m_{00}=\beta$, where $\beta$ is a predetermined value. Both invariance properties (for a binary image) can be achieved using : 
\begin{displaymath} h(x,y) = f \left( \frac{x}{a} + \overline{x},\frac{y}{a} + \... ...y} \right) ~~~~~\mbox{where $a = \sqrt{\frac{\beta}{m_{00}}}$} \end{displaymath}(58)

and $h(x,y)$ is the new translated and scaled function. The error involved in the discrete implementation can be reduced by interpolation. If the coordinate calculated by Equation 1.58 does not coincide with an actual grid location, the pixel value associated with it is interpolated from the four surrounding pixels. As a result of the normalisation, the Zernike moments $\mid A_{00} \mid$ and $\mid A_{11} \mid$are set to known values. $\mid A_{11} \mid$ is set to zero, due to the translation of the shape to the centre of the coordinate system. This however will be affected by a discrete implementation where the error in the mapping will decrease as the shape (being mapped) size (or pixel-resolution) increases. $\mid A_{00} \mid$ is dependent on $m_{00}$, and thus on $\beta$: 
\begin{displaymath} \mid A_{00} \mid ~= \frac{\beta}{\pi} \end{displaymath}(59)

Further, the absolute value of a Zernike moment is rotation invariant as reflected in the mapping of the image to the unit disc. The rotation of the shape around the unit disc is expressed as a phase change, if $\phi$ is the angle of rotation, $A_{mn}^R$ is the Zernike moment of the rotated image and $A_{mn}$ is the Zernike moment of the original image then: 
\begin{displaymath} A_{mn}^R = A_{mn}\exp(-jn\phi) \end{displaymath}(60)


Subsections
next up previous 
Next: A note on image Up: Orthogonal moments Previous: Legendre moments
Jamie Shutler 2002-08-15


저작자표시 비영리 동일조건

'Enginius > Machine Learning' 카테고리의 다른 글

ANN로 headPoseEstimate하기  (0) 2012.06.05
Markov Chain Monte Carlo (MCMC) and Gibbs Sampling example(MATLAB)  (0) 2012.05.31
푸리에 변환과 라플라스 변환  (18) 2012.05.01
Hierarchical Temporal Memory Prototype ver1.0.0  (4) 2012.04.26
기계 학습과 수학적 뒷받침  (0) 2012.04.26

'Enginius/Machine Learning' Related Articles

티스토리툴바